Copyright © 2006 Ron Catterall
| Revision History | |
|---|---|
| Revision 0.1 | 4 March 2006 |
|
Document generated on Saturday, 11 March, 2006 @ 11:06:58 |
|
This document is a re-working of the earlier document, moving the dates of the population estimates from the middle of the Danibaan (400 BC), Pe (200 BC) and Nisa (0 BC/AD) to the end of the periods (300 BC, 100 BC, and 100 AD respectively.)
When one has an estimate of population in a period, for example 5398 in the Danibaan, it is not obvious what date in the period to assign to that population figure, the beginning (500 BC), middle (400 BC) or end (300 BC) of the period. If we can accept 500 BC as the date of the founding of the settlement at Monte Albán, then we must reject the date of the start (500 BC) of the period. In the absence of any real evidence it might be best to accept the middle (400 BC) of the period, but if the estimate could be interpreted as “during the Danibaan period (500-300 BC) the population grew to 5398”, then we might be more justified in assigning the population (5398) to the end (300 BC) of the period. And similarly for the Pe and Nisa periods. Certainly the end of the periods is the more conservative approach since we are concerned with explaining the rapidity of growth.
| Period | Date (middle of period) | Date (end of period) | Population |
|---|---|---|---|
| There is no evidence for settlement at Monte Albán prior to 500 BC, and we set the population at the middle (600 BC) of the Rosario period to zero. | |||
| Rosario | 600 BC | 0 | |
| Rosario | 500 BC | 200 | |
| Danibaan | 400 BC | 300 BC | 5398 |
| Pe | 200 BC | 100 BC | 16630 |
| Nisa | 0 BC/AD | 100 AD | 14492 |
A second problem is the source of population growth, or at least the major part of it. There are two obvious sources, internal growth arising from expansion of the initial (foundation) population, and growth by accretion (immigration to Monte Albán.) If we find that the rate of growth is too high to be reasonably explained by internal growth, then we might assign the difference between a reasonable growth and the estimated growth to immigration. Just what is a reasonable growth rate for a newly founded colony is a matter of some conjecture; clearly it is not the rate observed for a modern industrialised society like the USA (5.34 per 1000 per year) or the UK (0.35 per 1000), or an essentially retirement community like the Isle of man (-0.14 per 1000.) Perhaps we should also exclude some African countries such as Niger (26.76 per 1000) which are receiving extensive external help. It is probably also unfair to draw a comparison with modern Mexico (17.09 per 1000) although it has a predominantly youthful population, or with a rapidly developing country like Papua New Guinea (21.60 per 1000.) We could take an average over countries reporting birth and death rates (about 225 of them at 9.96 per 1000 per year) or somewhat less reliable estimates for the entire world (11.43 per 1000 per year.) However, none of these are directly comparable to the situation in early Monte Albán where the population density was very low compared with the world today. Perhaps the best we can do is to estimate the rate of growth as something like the average of recorded rates today (9.96 per 1000,) with some generous error estimates, possibly between 5 and 15 per 1000.
Intuitively we would like to fit the population estimates for all periods with an initial foundation population somewhat less than the population (564) of San José Mogote in (at the end of) the Rosario period - perhaps somewhere in the range 200-500.
The population estimates in the above table show a slight decrease in the Nisa period. Fitting the full range of population estimates to a Weibull function leads to a steady population of about 15,700 between about 100 BC and 100 AD, and we take the population at the end of the Pe period as 15,700 in the following analysis.
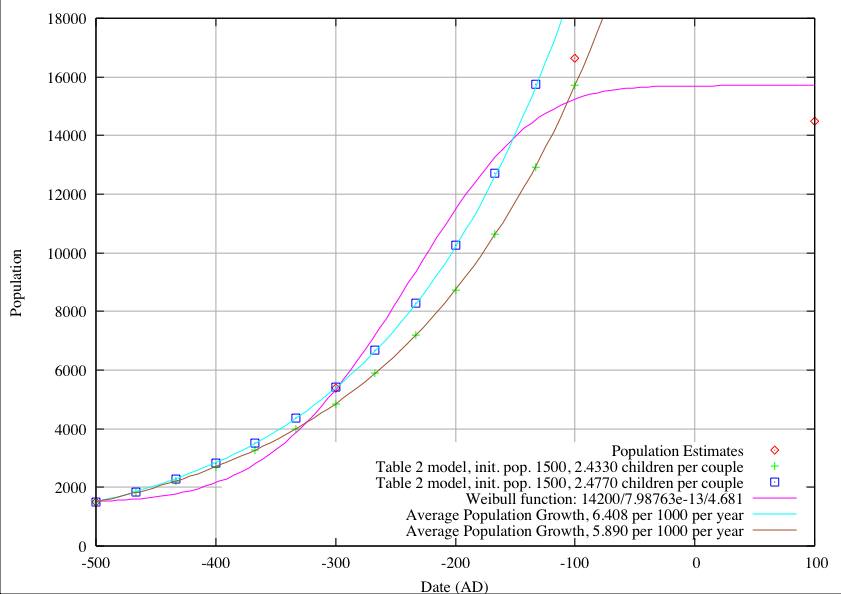
In the following 6 figures we compare the population estimates with 3 models for growth and for 6 estimates of initial foundation population, assuming that growth is entirely due to internal expansion. Calculated populations from the model of Winter, Table 2 are represented by points at each generation. Calculated populations using annual growth rates are represented by continuous lines, and the empirical Weibull growth function [1] is also a continuous line. The Winter model, given assumptions of generation span, average number of children per couple and no early deaths, is functionally identical with the model based on annual population growth. We assume a generation span of 33.33 years (3 generations per century) and adjust the number of children per pair to get the best fit to the population estimates. Similarly we adjust the annual population growth figure to get the same values.
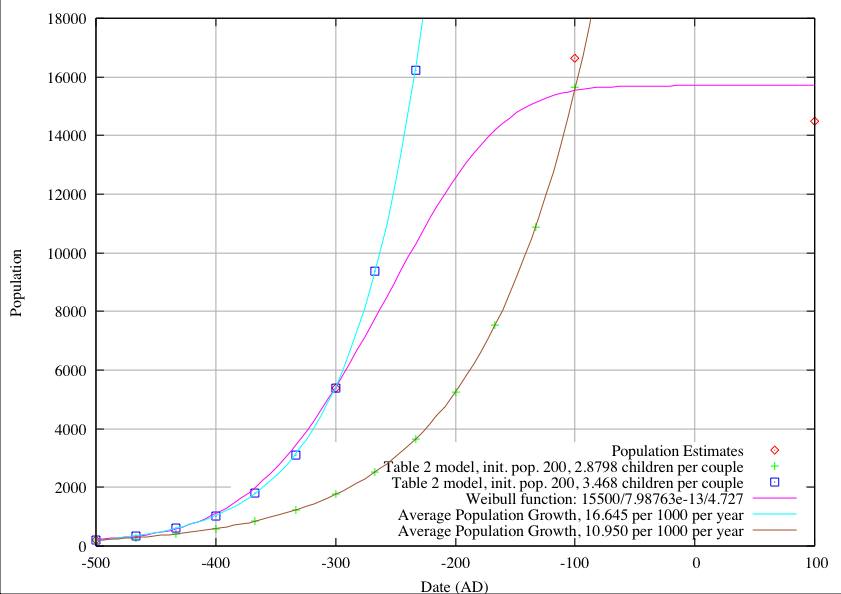
In the first figure we start with an initial population of 200 at 500 BC. Ignoring the Weibull function we find we cannot fit both the population estimates (at the end of the Danibaan and Pe periods) with a single value of children per couple or a yearly population growth, so we include 2 separate fits, one to the end of the Danibaan (3.46 children or 16.645 per 1000 years) and one to the end of the Pe (2.8798 children or 10.950 per 1000 years). The values of children and yearly growth are generally in reasonable accord with current population statistics. The Weibull function yields a very reasonable fit to the data, but with the exception of the limiting population of 15,700, the other two parameters ( a and b ) in the function have no physical significance (and have indeed have a very high pairwise correlation coefficient.)
The outstanding problem is that the Winter model cannot predict the population estimates at 500 BC, 300 BC and 100 BC for an initial population of 200. There is no way around this discrepancy as long as we attribute growth of population to an internal expansion. One obvious solution is to accept that once Monte Albán was recognised as a good or important place to live, other people from the valley floor started to move in and the population was swelled by continual immigration. Initially immigration is welcome, it enhances the wealth and power of the community. At some point, however, competition for increasingly scarce resources begins to discourage immigration, the community becomes less attractive to outsiders, and the insiders more aggressive. However, there is an alternative possibility to immigration: if the initial foundation population is increased, the growth curve to 300 BC becomes less steep and there is a likelihood that eventually the populations at 500 BC, 300 BC and 100 BC will all lie on the same Winter model line. We investigate this further by increasing the initial population in stages to 350, 500, 800 and 1,500.
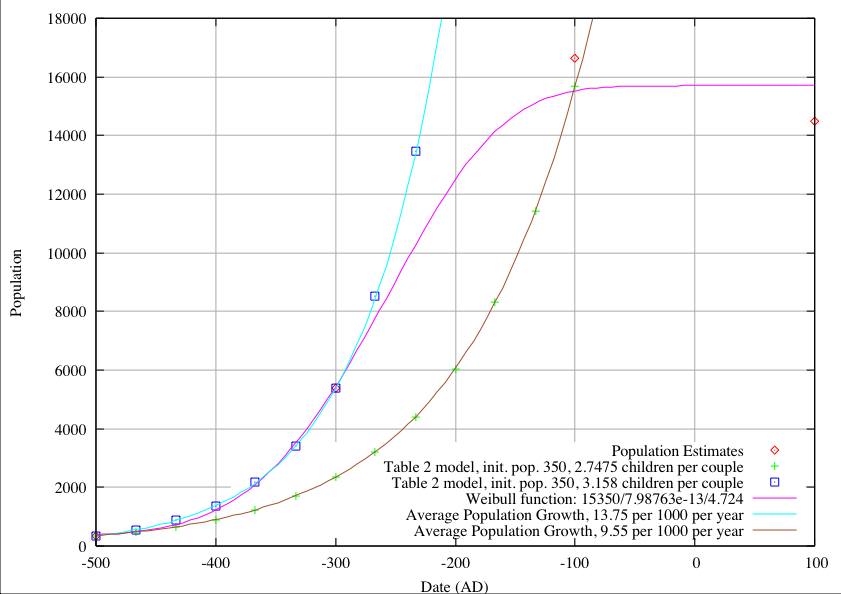
In the second figure we start with an initial population of 350 at 500 BC. Again ignoring the Weibull function we still find we cannot fit both the population estimates. The parameter values are collected in the table below.
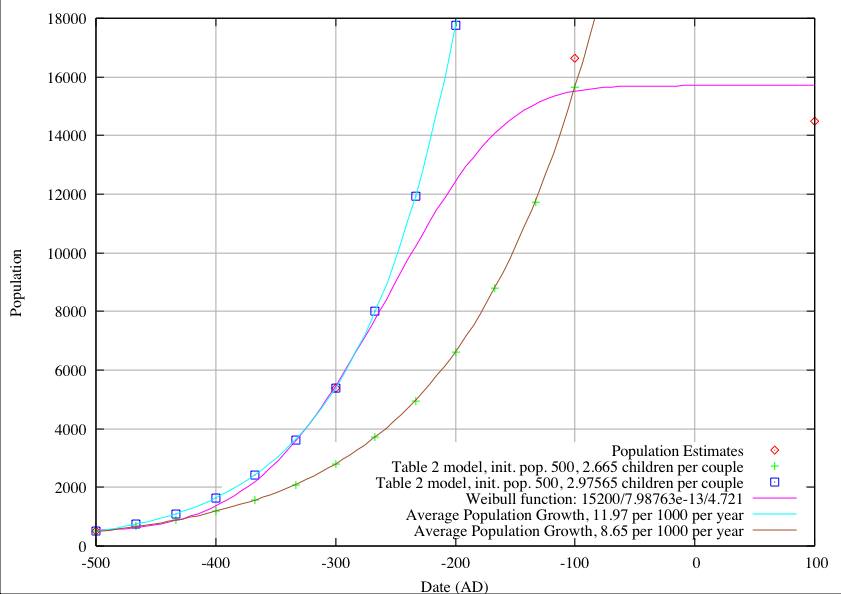
In the third figure we start with an initial population of 500 at 500 BC. Again ignoring the Weibull function we find we still cannot fit both the population estimates. Nevertheless it now becoming clear that as we increase the initial population, the fits to the two population estimates are becoming closer together. We now explore increasing the initial population above the value we regard as a reasonable upper limit.
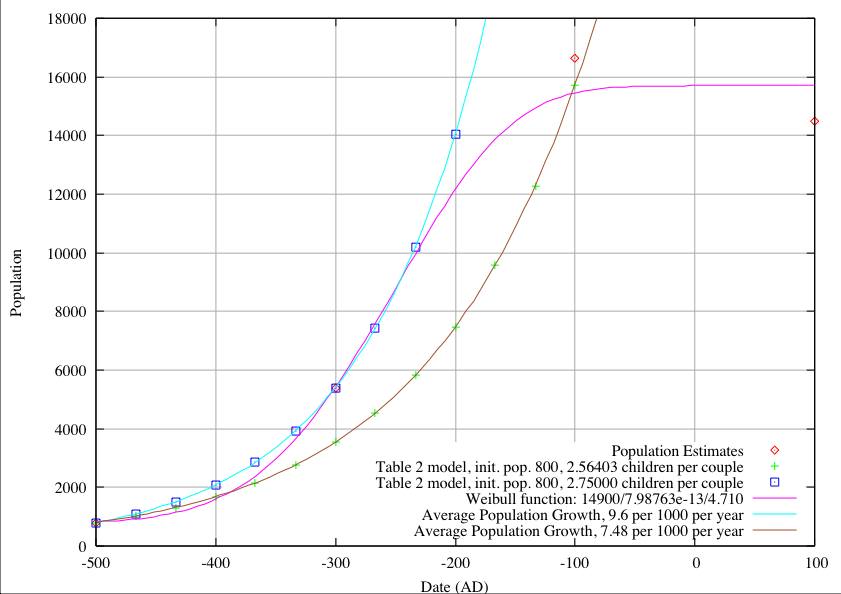
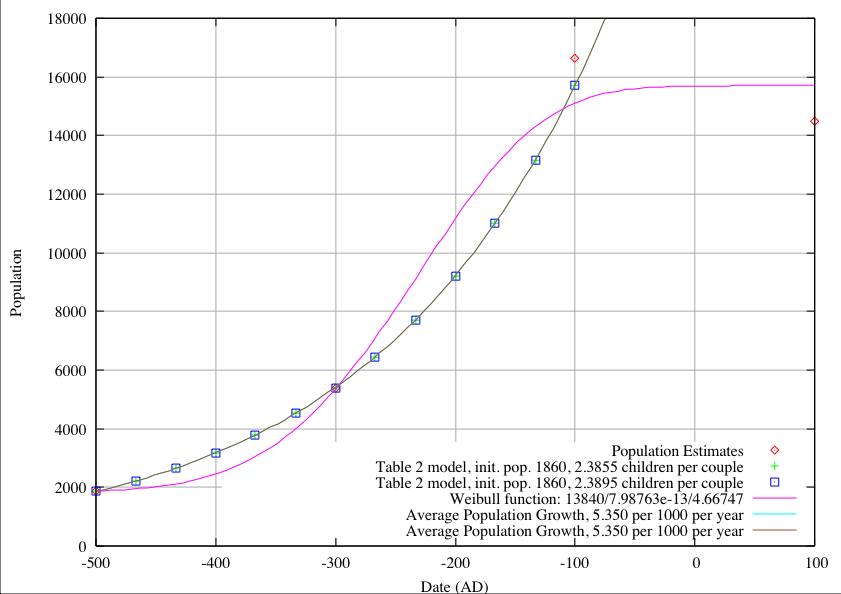
In Figures 4 and 5 we start with populations of 800 and 1,500 respectively and arrive at the same inability to fit population estimates at 300 BC and 100 BC. It is only when we set the initial population to 1860 in figure 6 that we are able to fit the data at both 300 BC and 100 BC.
| Initial Population | Fit to end Danibaan | Fit to end Pe | Weibull parameters | ||||
|---|---|---|---|---|---|---|---|
| children | growth | children | growth | Pmax | a | b | |
| 200 | 3.468 | 16.645 | 2.8798 | 10.950 | 15,500 | 7.98763-13 | 4.727 |
| 350 | 3.158 | 13.750 | 2.7475 | 9.550 | 15,350 | 7.98763-13 | 4.724 |
| 500 | 2.976 | 11.970 | 2.6650 | 8.650 | 15,200 | 7.98763-13 | 4.721 |
| 800 | 2.750 | 9.600 | 2.5640 | 7.480 | 14,900 | 7.98763-13 | 4.710 |
| 1500 | 2.477 | 6.408 | 2.4330 | 5.890 | 14,200 | 7.98763-13 | 4.681 |
| 1860 | 2.3855 | 5.3500 | 2.3855 | 5.350 | 13,840 | 7.98763-13 | 4.66747 |
Conclusion. If we accept that an initial foundation population much greater than about 500 is unacceptable, then we must conclude that the population figures at 300 BC and 100 BC cannot be explained by internal growth of the initial population. Certainly an initial population of 1860 seems completely out of the question. The only feasible explanation of the population at 300 BC is to assume additional immigration into Monte Albán during the period 500 BC to 300BC. Effectively, at 300 BC, the progeny of the initial foundation group would only account for about one third of the population. After 300 BC, either immigration or birth rate would have to slow down very appreciably in order to reach a population of around 15,700 at 100 BC. We have no reason to anticipate a large reduction in birth rate, so we have to postulate either a higher death rate (war?) or an end to immigration. The Weibull function produces a very reasonable fit to the data and suggests very strongly that after 300 BC there is an increasing restraint acting against population growth. The restraint could be attributed to war (the first appearance of fortifications at Monte Albán) or possibly to a general shortage of resources (primarily food and water) on the hill top. Shortage of resources does not seem to be very likely, the valley has sufficient fertile ground to support a much larger population. War and strife within the valley might restrain growth, San José Mogote, Yegüih and Tilcajete all grew significantly in the Danibaan period (Winter, Table 1.) There is no obvious threat from outside the valley at this time.
We must also bear in mind that the population estimates might be subject to considerable possible error, but accepting the figures as having some value, we have determined that:
-
There was a significant drift of population from the valley to Monte Albán during the period 500 BC to 300 BC. It remains to be determined exactly where the immigrants came from. It is clear that the populations of San José Mogote, Yegüih and Tilcajete were also growing in this period, whilst the number of small settlements was also growing.
-
There was a significant restraint on growth of population at Monte Albán during the period 300 BC to 100 BC. It seems most likely that this was strife internal to the valley and was coincident with the deployment of some defensive structures at Monte Albán.
-
There was little or no growth in the population of Monte Albán during the period 100 BC to 100 AD. Possibly this is indicative of a lack of control over the whole valley by the inhabitants of Monte Albán.
The whole argument in this work rests on the estimated population of Monte Albán at 300 BC, if that were a serious over-estimate, and the population was actually around 1800, the Winter model would explain the growth very adequately on the basis of internal expansion alone. The possibility that the initial foundation population was as high as 1860 seems exceedingly remote.
[1] Pt = Pmax(1-exp(-a(tb)))
where Pt is the population at time t , Pmax is the maximum population attained, and a and b are constants determined in the fit of the function to the growth data.
which we normalise to a given population at 500BC, zero population at 600BC and a constant population of 15,700 after about 100 BC
Pt = P500 + Pmax(1-exp(-a(t+600)b)))
where P500 is the initial foundation population at 500 BC, Pmax is now 15,700-P500 and the population is zero at 600 BC.